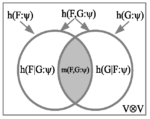
This paper gives a new derivation of the variance (and covariance) based on the two-sample approach, which positions the variance on the partition and information theory side of the duality and thus dual to the mean.
A new logical measure for quantum information
March 15, 2025 by
Logical entropy is compared and contrasted with the usual notion of Shannon entropy. Then a semi-algorithmic procedure (from the mathematical folklore) is used to translate the notion of logical entropy at the set level to the corresponding notion of quantum logical entropy at the (Hilbert) vector space level.
A Fundamental Duality in the Mathematical and Natural Sciences
September 8, 2024 by
This is an essay in what might be called “mathematical metaphysics.” There is a fundamental duality that runs through mathematics and the natural sciences, from logic to biology.
A Basic Duality in the Exact Sciences: Application to QM
May 12, 2024 by
This approach to interpreting quantum mechanics is not another jury-rigged or ad-hoc attempt at the interpretation of quantum mechanics but is a natural application of the fundamental duality running throughout the exact sciences.
A Pedagogical Model of Quantum Mechanics Over Sets
April 9, 2024 by
The new approach to quantum mechanics (QM) is that the mathematics of QM is the linearization of the mathematics of partitions (or equivalence relations) on a set. This paper develops those ideas using vector spaces over the field Z2 = {0.1} as a pedagogical or toy model of (finite-dimensional, non-relativistic) QM.
New Logic & New Approach to QM
March 17, 2024 by
The new logic of partitions is dual to the usual Boolean logic of subsets (usually presented only in the special case of the logic of propositions) in the sense that partitions and subsets are category-theoretic duals. The new information measure of logical entropy is the normalized quantitative version of partitions. The new approach to interpreting quantum mechanics (QM) is showing that the mathematics (not the physics) of QM is the linearized Hilbert space version of the mathematics of partitions. Or, putting it the other way around, the math of partitions is a skeletal version of the math of QM.
The new partitional approach to (literally) interpreting quantum mechanics
May 1, 2023 by
This paper presents a new `partitional’ approach to understanding or interpreting standard quantum mechanics (QM). The thesis is that the mathematics (not the physics) of QM is the Hilbert space version of the math of partitions on a set and, conversely, the math of partitions is a skeletonized set level version of the math of QM.
“Follow the Math” Preprint
February 26, 2023 by
The slogan “Follow the money” means that finding the source of an organization’s or person’s money may reveal their true nature. In a similar sense, we use the slogan “Follow the math!” to mean that finding “where the mathematics of QM comes from” reveals a good deal about the key concepts and machinery of the theory.
Partitions, Objective Indefiniteness, and Quantum Reality
December 30, 2022 by
This paper, published in the International Journal for Quantum Foundations, is a shorter introductory paper following up on my recent “Follow the Math!” paper in the Foundations of Physics. The point is to show that the mathematics of QM is the vector (Hilbert) space version of the mathematics of partitions at the set level. […]