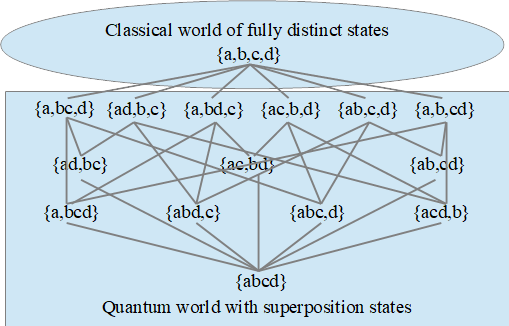
This paper, published in the International Journal for Quantum Foundations, is a shorter introductory paper following up on my recent “Follow the Math!” paper in the Foundations of Physics. The point is to show that the mathematics of QM is the vector (Hilbert) space version of the mathematics of partitions at the set level. Since partitions are the math tool to describe indefiniteness and definiteness, this shows how the reality so well described by QM is a non-classical reality featuring the objective indefiniteness of superposition states. The lattice of partitions gives a skeletal model of quantum reality with the partition versions of pure states, non-classical mixed states (i.e., including a superposition state), and the completely distinguished classical state that satisfies the partition logic version of the Principle of Identity of Indistinguishables. Both the key notions of quantum states and quantum observables are the (density) matrix versions of partitions and vector space version of a numerical attributes. The operation of projective measurement given by the Luders mixture operation is the vector space version of the partition join operation between the partition prefiguring the density matrix of the state being measured and the partition prefiguring the observable being measured. All this adds specificity to Shimony’s idea of a literal interpretation to form what might be called the “objective indefiniteness interpretation” of QM–since it is the notion of a superposition as being (objectively) indefinite between the superposed eigenstates that replaces the usual “sum of waves” interpretation of superposition.