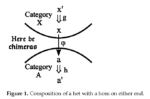
The new logic of partitions is dual to the usual Boolean logic of subsets (usually presented only in the special case of the logic of propositions) in the sense that partitions and subsets are category-theoretic duals. The new information measure of logical entropy is the normalized quantitative version of partitions. The new approach to interpreting quantum mechanics (QM) is showing that the mathematics (not the physics) of QM is the linearized Hilbert space version of the mathematics of partitions. Or, putting it the other way around, the math of partitions is a skeletal version of the math of QM.
Heteromorphic Approach to Adjunctions
Saunders Mac Lane famously remarked that “Bourbaki just missed” formulating adjoints in a 1948 appendix (written no doubt by Pierre Samuel) to an early draft of Algebre–which then had to wait until Daniel Kan’s 1958 paper on adjoint functors. But Mac Lane was using the orthodox treatment of adjoints that only contemplates the object-to-object morphisms […]
The Born Rule is a feature of Superposition
The Born Rule arises naturally out of the mathematics of probability theory enriched by superposition events. It does not need any more-exotic or physics-based explanation. No physics was used in the making of this paper. The Born Rule is just a feature of the mathematics of superposition.
Kaldor-Hicks Petitio Principii Fallacy
This paper shows that implicit assumptions about the numeraire good in the Kaldor–Hicks efficiency–equity analysis involve a ‘‘same-yardstick’’ fallacy (a fallacy pointed out by Paul Samuelson in another context), a special case of the Petitio Pricipii fallacy.
The new partitional approach to (literally) interpreting quantum mechanics
This paper presents a new `partitional’ approach to understanding or interpreting standard quantum mechanics (QM). The thesis is that the mathematics (not the physics) of QM is the Hilbert space version of the math of partitions on a set and, conversely, the math of partitions is a skeletonized set level version of the math of QM.
“Follow the Math” Preprint
The slogan “Follow the money” means that finding the source of an organization’s or person’s money may reveal their true nature. In a similar sense, we use the slogan “Follow the math!” to mean that finding “where the mathematics of QM comes from” reveals a good deal about the key concepts and machinery of the theory.
Partitions, Objective Indefiniteness, and Quantum Reality
This paper, published in the International Journal for Quantum Foundations, is a shorter introductory paper following up on my recent “Follow the Math!” paper in the Foundations of Physics. The point is to show that the mathematics of QM is the vector (Hilbert) space version of the mathematics of partitions at the set level. […]
Abstraction in Math and Superposition in QM
Abstraction turns equivalence into identity, but there are two ways to do it. The goal is to use the second notion of abstraction to shed some light on the notion of an inde finite superposition in quantum mechanics.
4Open: Special Issue: Intro. to Logical Entropy
4Open is a relatively new open access interdisciplinary journal (voluntary APCs) covering the 4 fields of mathematics, physics, chemistry, and biology-medicine. A special issue on Logical Entropy was sponsored and edited by Giovanni Manfredi, the Research Director of the CNRS Strasbourg. My paper is the introduction to the volume.
Book Draft: The Logic of Partitions
This book draft is an introduction to the logic of partitions on a set as well as the (quantum) logic of partitions (direct-sum decompositions or DSDs) on a vector space.