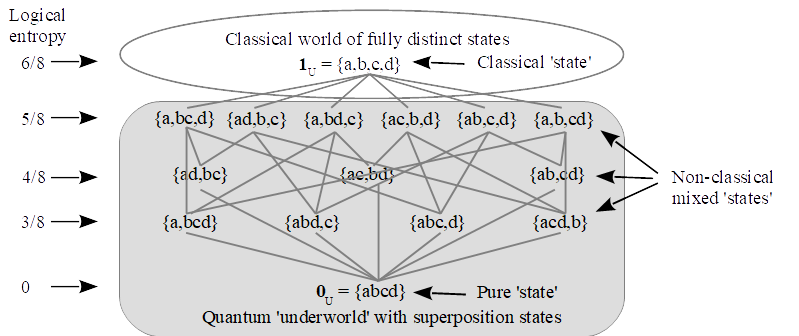
This paper presents a new `partitional’ approach to understanding or interpreting standard quantum mechanics (QM). The thesis is that the mathematics (not the physics) of QM is the Hilbert space version of the math of partitions on a set and, conversely, the math of partitions is a skeletonized set level version of the math of QM. Since at the set level, partitions are the mathematical tool to represent distinctions and indistinctions (or definiteness and indefiniteness), this approach shows how to interpret the key non-classical QM notion of superposition in terms of (objective) indefiniteness between definite alternatives (as opposed to seeing it as the sum of `waves’). Hence this partitional approach substantiates what might be called the Objective Indefiniteness Interpretation or what Abner Shimony called the Literal Interpretation of QM. In a slogan: Quantum reality is indefinite-world, not wave-world.