This paper attempts set forth systematically some of the knowledge questions that determine certain strategies for institutional change.
My Congressional Testimony on Iraq in 2003
November 6, 2016 by
This is my testimony to the Joint Economic Committee of Congress in 2003 making recommendations after the U.S. conquered Iraq and had to figure out what to do. Today, it can be read as a negative-blueprint since the U.S. seems to have done just the opposite on every count.
Autonomy-Respecting Assistance
October 9, 2016 by
This paper, written upon request for the UNDP volume on Capacity for Development and in time for a big conference in Mexico on the topic, is a good brief summary of my then forthcoming book, Helping People Help Themselves –even if I was screwed out of a sizable honorarium by one of the editors, Malik.
Helping People Help Themselves
December 19, 2012 by
The full title to this book is: Helping People Help Themselves: From
the World Bank to an Alternative Philosophy of Development Assistance. The book is an intellectual analysis, giving a full history of the relevant ideas, of the various modes of “helping” in general and development assistance in particular.
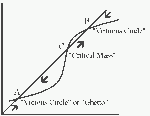
Revisiting Hirschman
December 15, 2012 by
This paper revisits the seminal early work of the late Albert Hirschman on development strategy and his critique of the “big push” strategies in order to elucidate the current debates about conditionality-based aid and comprehensive development programs.
Mixing Truth & Power: A Guest Editorial
December 11, 2012 by
After the dissent-motivated departures of Joseph Stiglitz, Ravi Kanbur, and now Bill Easterly, even “the most casual observer” can begin to “connect the dots” and see that the Bank is having a problem handling dissent and criticism coming from internal sources. This editorial in the World Bank Staff Association Newsletter traces the problem to the organizational stance of taking “Official Views” on the complex questions of development–thereby mixing power and truth to the detriment of the latter.
Getting the bugs out of the Knowledge Bank
December 11, 2012 by
This note argues that the World Bank should base the Knowledge Bank on the way human learn, not the way insects learn.
World Bank survey paper on migration
December 10, 2012 by
This survey of the literature on migration and development was my last written product before retiring from the World Bank. But the results of years of documented experience is that migration leads to poverty alleviation (remittances) but not development. This is not the message that the Bank wants to hear so the results are largely ignored.
Should Development Agencies Have Official Views?
December 10, 2012 by
The major development agencies have ex cathedra “Official Views” (with varying degrees of explicitness) on the complex and controversial questions of development. At the same time, knowledge is now more than ever recognized as key to development—in the idea of a “knowledge bank” or knowledge-based development assistance. I argue that these two practices are in direct conflict—much as making Lysenko’s views as “Official Soviet Science” was in conflict with the progress of the science of genetics in the Soviet Union. When an agency attaches its “brand name” to certain Official Views, then it is very difficult for the agency to also be a learning organization or to foster genuine learning in the clients.
Helping People Help Themselves: Towards a Theory of Autonomy-Compatible Help
December 10, 2012 by
This is a presis of my book Helping People Help Themselves: From the World Bank to an Alternative Philosophy of Development Assistance. (U. of Michigan Press, 2005) I explore several principles or themes of a theory of autonomy-compatible assistance and show how these themes arise in the work of various authors in rather different fields.