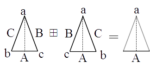
Semiadjunctions (essentially a formulation of universal mapping properties using hets) can be recombined in a new way to define the notion of a brain functor that provides an abstract model of the intentionality of perception and action (as opposed to the passive reception of sense-data or the reflex generation of behavior).
Logical Information Theory: New Foundations for Information Theory
There is a new theory of information based on logic. The definition of Shannon entropy as well as the notions on joint, conditional, and mutual entropy as defined by Shannon can all be derived by a uniform transformation from the corresponding formulas of logical information theory.
Logical Entropy: Introduction to Classical and Quantum Logical Information Theory
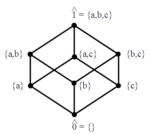
Logical information theory is the quantitative version of the logic of partitions just as logical probability theory is the quantitative version of the dual Boolean logic of subsets. The resulting notion of information is about distinctions, differences, and distinguishability, and is formalized as the distinctions of a partition (a pair of points distinguished by the partition). This paper is an introduction to the quantum version of logical information theory.
Quantum Logic of Direct-sum Decompositions
The usual quantum logic, beginning with Birkhoff and Von Neumann, was the logic of closed subspaces of a Hilbert space. This paper develops the more general logic of direct-sum decompositions of a vector space. This allows the treatment of measurement of any self-adjoint operators rather than just the projection operators associated with subspaces.
From Abstraction in Math to Superposition in QM
This is a draft paper that makes a perhaps surprising connection between the old Platonic notion of a paradigm-universal like ‘the white thing’ and an indefinite superposition state in quantum mechanics.
On Classical and Quantum Logical Entropy: The analysis of measurement
This paper shows how classical and quantum logical entropy arise out of the logic of partitions, and then it shows how there is a natural connection between the nxn distinctions and indistinctions of a partition and the nxn entries in a density matrix so that the classical and quantum logical entropy can directly register what happens to the density matrix in a projective measurement. The standard notion of von Neumann entropy does nothing of the kind–so the paper is also an indirect critique of von Neumann entropy as the most natural and ‘informative’ notion of entropy to use in quantum information theory.
Category theory and set theory as theories about complementary types of universals
This is a paper, published in Logic and Logical Philosophy, on the concept of universals in philosophical logic–which includes the example of “Sophia Loren as “the” Italian women”. The always-self-predicative universals of category theory form the opposite bookend to the never-self-predicative universals of iterative set theory.
Quantum Mechanics over Sets
This paper published in Synthese shows how the classical finite probability theory (with equiprobable outcomes) can be reinterpreted and recast as the quantum probability calculus of a pedagogical or “toy” model of quantum mechanics over sets (QM/sets).
Gian-Carlo Rota’s Probability Course: The Guidi Notes
This is a copy of the Guidi Notes for Gian-Carlo Rota’s Probability course at MIT the last time Rota gave the course. A copy of the Rota-Baclawski text used as course material can also be downloaded here.
Gian-Carlo Rota’s Combinatorial Theory Course: The Guidi Notes
This is a copy of the Guidi Notes for Gian-Carlo Rota’s famous Combinatorial Theory course at MIT taken the last time Rota taught the course.