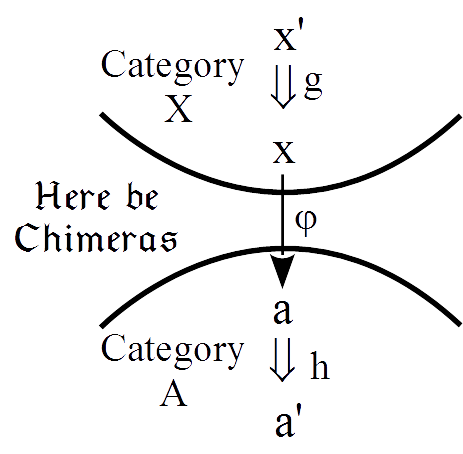These are the slides from a talk on the role of heteromorphisms (hets) in category theory given at the Category Theory Seminar at NYU on January 13, 2016. The talk starts with interpreting the elements in the values of het bifunctors (a.k.a. distributors, profunctors, bimodules) as object-to-object morphisms between the objects of different categories. This allows the “clearest” and simplest characterization of adjoints first given by Bodo Pareigis in 1969. It also highlights the basic nature of representable functors and universal mapping properties–as emphasized by the French-Grotendieck School–as opposed to the emphasis on adjoint functors in the American-MacLane School of category theory. Finally, the notion of a brain functor is introduced as having some application in cognitive science.
The Joy of Hets (talk slides)
February 29, 2016 by