The notion of a partition on a set is mathematically dual to the notion of a subset of a set, so there is a logic of partitions dual to Boole’s logic of subsets (Boolean subset logic is usually mis-specified as the special case of “propositional” logic). The notion of an element of a subset has as its dual the notion of a distinction of a partition (a pair of elements in different blocks). Boole developed finite logical probability as the normalized counting measure on elements of subsets so there is a dual concept of logical entropy which is the normalized counting measure on distinctions of partitions. Thus the logical notion of information is a measure of distinctions. Classical logical entropy also extends naturally to the notion of quantum logical entropy which provides a more natural and informative alternative to the usual von Neumann entropy in quantum information theory. The quantum logical entropy of a post-measurement density matrix has the simple interpretation as the probability that two independent measurements of the same state using the same observable will have different results.
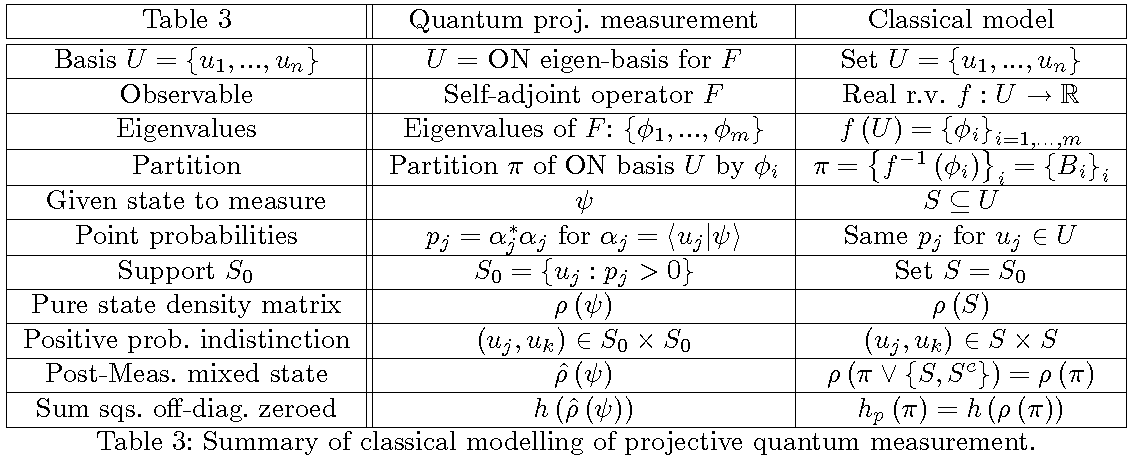
The main result of the paper is that this increase in quantum logical entropy due to a projective measurement of a pure state is the sum of the absolute squares of the off-diagonal entries (`coherences’) of the pure state density matrix that are zeroed (decohered) by the measurement, i.e., the measure of the distinctions (`decoherences’) created by the measurement. The von Neumann entropy provides no such analysis of measurement. That result is also classically modeled using ordinary partitions and density matrices for such partitions in the pedagogical model of QM/Sets with point probabilities–which for a fixed basis is just sampling a real r.v. in classical finite probability theory.