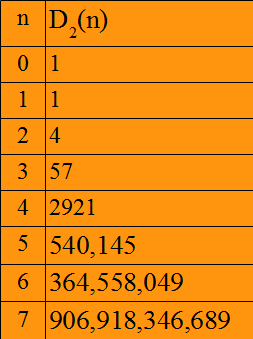
The theory of q-analogs develops many combinatorial formulas for finite vector spaces over a finite field with q elements–all in analogy with formulas for finite sets (which are the special case of q=1). A direct-sum decomposition of a finite vector space is the vector space analogue of a set partition. This paper uses elementary methods to develop the formulas for the number of direct-sum decompositions that are the q-analogs of the formulas for: (1) the number of set partitions with a given number partition signature; (2) the number of set partitions of an n-element set with m blocks (the Stirling numbers of the second kind); and (3) for the total number of set partitions of an n-element set (the Bell numbers). The paper also develops the formulas to enumerate: (4) the number of direct-sum decompositions in an n-dimensional vector space over GF(q) with m blocks and where any given nonzero vector is in one of the blocks, and (5) the number of direct-sum decompositions in an n-dimensional vector space over GF(q) where any given nonzero vector is in one of the blocks. The formulas for (2), (3), (4), and (5) generate integer sequences that were added as new sequences A270880-A270883 to the Online Encyclopedia of Integer Sequences.