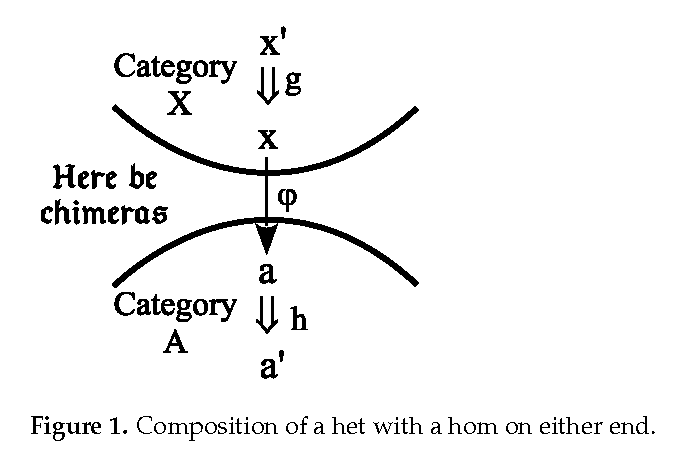
Saunders Mac Lane famously remarked that “Bourbaki just missed” formulating adjoints in a 1948 appendix (written no doubt by Pierre Samuel) to an early draft of Algebre–which then had to wait until Daniel Kan’s 1958 paper on adjoint functors. But Mac Lane was using the orthodox treatment of adjoints that only contemplates the object-to-object morphisms within a category, i.e., homomorphisms or homs. When Samuel’s treatment is reconsidered in view of the treatment of adjoints using heteromorphisms or hets (object-to-object morphisms between objects in different categories), then he, in effect, isolated the concept of a left representation solving a universal mapping problem. When dualized to obtain the concept of a right representation, the two halves only need to be united to obtain an adjunction. Thus Samuel was only a now-simple dualization away for formulating adjoints in 1948. Apparently, Bodo Pareigis’ 1970 text was the first and perhaps only text to give the heterodox “new characterization” (i.e., heteromorphic treatment) of adjoints. Orthodox category theory uses various relatively artificial devices to avoid formally recognizing hets–even though hets are routinely used by the working mathematician. Finally we consider a “philosophical” question as to whether the most important or basic concept in category theory is the notion of an adjunction (Mac Lane) or the notion of a representable functor (Grothendieck)–which solves a universal mapping problem, and where adjunctions arise as the special case of a bi-representation of dual universal mapping problems.
This paper appears in a special issue of Mathematics on Physical Geometry since adjunctions play an important role in the Zafiris approach.
Click here to download the article from the journal Mathematics.