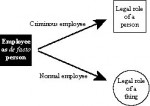
What is the inalienable rights theory that descends from the Reformation through the Enlightenment and that answers the classical apologies for slavery and autocracy based on implicit or explicit voluntary contracts?
Why was Slavery Wrong? Involuntariness or Treating Persons as Things?
February 28, 2010 by
“Involuntariness” is the usual answer.
Indeed, classical liberalism takes the most basic framing of a social question as: “consent or coercion?” In this view, democracy is characterized as government “with the consent of the governed” so slavery and non-democratic government were both condemned for the lack of consent.
This common condemnation of slavery on the basis of involuntariness has caused a large amount of intellectual history to just go “down the memory hole.” Those who routinely condemn involuntary slavery have either forgotten or never knew that from Antiquity down almost to the present there have always been those pro-slavery writers who: (1) presented a defense of slavery based on consent or contract, and (2) interpreted much of historical slavery as being based on implicit or explicit contracts.
My focus here is not on (2), the empirical question of whether or not any historical slavery could be interpreted as being voluntary, but (1), the fact of intellectual history that so many classical authorities defended slavery if based on consent.
History of the Logical Entropy Formula
February 16, 2010 by
The logical entropy formula Given a partition on a finite universe set U, the set of distinctions or dits is the set of ordered pairs of elements in distinct blocks of the partition. The logical entropy of the partition is the normalized cardinality of the dit set: . The logical entropy can be interpreted probabilistically […]
Arbitrage and Graphical Gridlock
February 9, 2010 by
The arbitrage-free law (or Kirchhoff’s voltage law) Recently I emailed a friend to complain when his organization used this 3 gear image as their logo. What was my complaint? Read on. The basic idea of arbitrage is to “get something for nothing” by trading commodities or currencies around some circle ending up with more than […]
From Partition Logic to Information Theory
February 6, 2010 by
A new logic of partitions has been developed that is dual to ordinary logic when the latter is interpreted as the logic of subsets rather than the logic of propositions. For a finite universe, the logic of subsets gave rise to finite probability theory by assigning to each subset its relative cardinality as a Laplacian probability. The analogous development for the dual logic of partitions gives rise to a notion of logical entropy that is related in a precise manner to Claude Shannon’s entropy.
Series-Parallel Duality: Part II: Financial arithmetic
February 5, 2010 by
In financial arithmetic and in the appraisal literature, it has been noticed that the basic formulas occur in pairs, one being the reciprocal of the other. This Part II of the series-parallel duality post shows that these reciprocal formulas are an example of the SP duality normally associated with electrical circuit theory.
The fatal flaw in finance theory: Capitalizing “goodwill”
February 5, 2010 by
The fatal flaw at the root of today’s post is really what might be called “the fundamental myth” about the current property system, namely that the market-contractual role of being the residual claimant in a productive opportunity is treated as a “property right” that is currently owned by some legal party (e.g., the corporation having the contractual role) and that may be bought and sold as well as capitalized into the party’s current valuation.
Series-Parallel Duality: Part I: Combating Series Chauvinism
February 4, 2010 by
This post describes the duality between the usual (series) addition and the dual parallel addition. This duality is normally considered in electrical circuit theory and combinatorics, but it has a much wider applications. In Part I of this post, the focus is on developing series-parallel dual formulas—in contrast to the usual focus on formulas using only the series sum.
The Math of Double-Entry Bookkeeping: Part I (scalars)
February 3, 2010 by
Double-entry bookkeeping illustrates one of the most astonishing examples of intellectual insulation between disciplines—the very opposite of intellectual trespassing.