Listing of talks and papers from 2013.
Introduction to Partition Logic
January 1, 2014 by
This is an introductory treatment of partition logic which also shows the extension to logical information theory and the possible killer application to quantum mechanics.
Introduction to Logical Entropy
November 24, 2013 by
This paper, a reprint from the International Journal of Semantic Computing, introduces the logical notion of entropy based on the newly developed logic of partitions that is mathematically dual to the usual Boolean logic of subsets (aka “propositional logic”), and compares it to the usual Shannon entropy.
Information as distinctions
January 23, 2013 by
This paper is sub-titled “New Foundations for Information Theory” since it is based on the logical notion of entropy from the logic of partitions. The basic logical idea is that of “distinctions.” Logical entropy is normalized counting measure of the set of distinctions of a partition, and Shannon entropy is the number of binary partitions needed, on average, to make the same distinctions of the partition.
Counting Distinctions
December 11, 2012 by
This paper gives the logical theory of information that is developed out of partition logic in exactly the same way that Boole developed logical probability theory out of his subset logic.
Seminar in Quantum Information Theory II
December 10, 2012 by
These are the slides from a seminar in quantum information theory and related topics in the Computer Science Department of UC/Riverside during the Spring quarter 2012.
Seminar in Quantum Information Theory I
December 10, 2012 by
These are the slides from a seminar in quantum information theory taught in the Computer Science Department of UC/Riverside in the Winter quarter 2012.
The Objective Indefiniteness Interpretation of Quantum Mechanics
October 31, 2012 by
The purpose of this blog entry is to briefly describe a new interpretation of quantum mechanics (QM). A long paper introducing this objective indefiniteness interpretation is available at the Quantum Physics ArXiv and (a more recent version) on my website.
History of the Logical Entropy Formula
February 16, 2010 by
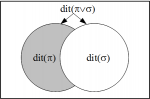
The logical entropy formula Given a partition on a finite universe set U, the set of distinctions or dits is the set of ordered pairs of elements in distinct blocks of the partition. The logical entropy of the partition is the normalized cardinality of the dit set: . The logical entropy can be interpreted probabilistically […]
From Partition Logic to Information Theory
February 6, 2010 by
A new logic of partitions has been developed that is dual to ordinary logic when the latter is interpreted as the logic of subsets rather than the logic of propositions. For a finite universe, the logic of subsets gave rise to finite probability theory by assigning to each subset its relative cardinality as a Laplacian probability. The analogous development for the dual logic of partitions gives rise to a notion of logical entropy that is related in a precise manner to Claude Shannon’s entropy.