The Objective Indefiniteness Interpretation of Quantum Mechanics

Introduction

The purpose of this blog entry is to briefly describe a new interpretation of quantum mechanics (QM). A long paper introducing this objective indefiniteness interpretation is available at the Quantum Physics ArXiv and (a more recent version) on my website. The notion of objective indefiniteness has been emphasized by Abner Shimony.

From these two basic ideas alone — indefiniteness and the superposition principle — it should be clear already that quantum mechanics conflicts sharply with common sense. If the quantum state of a system is a complete description of the system, then a quantity that has an indefinite value in that quantum state is objectively indefinite; its value is not merely unknown by the scientist who seeks to describe the system. … Classical physics did not conflict with common sense in these fundamental ways. [Shimony 1988, p. 47]

Subset logic and partition logic

This interpretation of QM grew out of work in mathematical logic that was developed without any thought of a connection with quantum mechanics. The basic system of ordinary logic, which is now almost invariably called “propositional” logic, was originally developed mainly by George Boole. But Boole developed the system as the logic of subsets, with the application to propositions being a special case, albeit an important special case.

The algebra of logic has its beginning in 1847, in the publications of Boole and De Morgan. This concerned itself at first with an algebra or calculus of classes,… a true propositional calculus perhaps first appeared…in 1877. [Church 1956, p. 155-156]

A tautology or logically valid formula of subset logic is a formula so that no matter what subsets of a nonempty fixed universe U are substituted for the variables, when the subset operations in the formula (e.g., join, meet, implication) are applied, the whole formula evaluates to U. It turns out that to determine validity, it suffices to consider only a singleton set U = 1, which has only two subsets 0 (the empty set) and 1. In that special case, a formula can be evaluated using the truth tables of any elementary logic course. Thus there is a theorem, known to Boole, that if a formula is a truth table tautology, then it is a tautology (where the reverse holds trivially). This theorem then facilitated taking the special case of interpreting the variables as propositions (with 0 and 1 truth values) rather than subsets as the whole of the logic instead on a special case, and hence the name “propositional” logic. That confusion of the part with the whole is now standard in all the logic texts so that, for instance, the truth table notion of a tautology is now taken as the definition (rather than a theorem in subset logic).

Why is the reduction of subset logic to the special case of propositional logic a problem? It is a problem because the concept of a subset (or more generally a subobject) has a mathematical dual in the concept of a quotient set (or equivalence relation or partition). This duality is seen throughout abstract algebra in the duality of subobjects (e.g., subgroups, subrings, etc.) and quotient objects. The mathematical basis for this duality is captured by category theory and is known as the “reverse the arrows” category-theoretic duality. In the case at hand, William Lawvere calls the general notion of a subobject a “part” and then he and Rosebrugh note:

The dual notion (obtained by reversing the arrows) of “part” is the notion of partition. [Lawvere and Rosebrugh 2003, p. 85]

In contrast, the ordinary notion of a proposition does not have a dual.

When logic is seen as the Boolean logic of subsets in the context of the modern notion of category-theoretic duality, then the question would immediately arise of a dual logic of partitions. But since logic was typically seen as “propositional” logic, the idea of a dual logic of partitions was not “in the air.”

Since the nineteenth century, it was known that equivalence relations form a lattice, and those lattices have been much studied in combinatorial theory. But there have been some infelicities. Although often called “lattices of partitions,” the lattices studied in combinatorial theory are usually written upside down (for the purposes of partition logic). Moreover, one would think that a “logic” [Finberg et al. 1996] would have an implication operation, but the attention has been restricted to the lattice operations of join and meet. As late as 2001, it was noted that:

the only operations on the family of equivalence relations fully studied, understood and deployed are the binary join $\vee$ and meet $\wedge$ operations. [Britz et al. 2001, p. 445]

Thus for a variety of reasons, e.g., subset logic seen as “propositional” logic, lattice of partitions written upside down, and only join and meet operations studied, the development of partition logic was long delayed.

Once partition logic is developed, then just as Boole defined logical finite probability theory on top of subset logic, so the analogous moves applied to the logic of partitions yields a logical notion of information content or logical entropy. Those moves from partition logic to logical information theory were described in a previous blog.

Two lattices and two creation stories

For subset logic, the lattice is the Boolean lattice of subsets of a fixed nonempty universe set U. The elements in the lattice are all the subsets of U ordered by inclusion. The join is the union of subsets and the meet is the intersection of subsets. The top is the universe U and the bottom is the empty set.

For partition logic, the lattice is the lattices of partitions on a fixed universe U where the ordering is refinement. In more technical terms, a partition $\pi = \{B,B',\ldots\}$ on a universe set U (two or more elements to avoid degeneracy) is a set of non-empty subsets (“blocks”) $B,B',\ldots \subseteq U$ that are disjoint and jointly exhaust U. A partition $\sigma = \{C,C',\ldots \}$ is refined by a partition $\pi = \{B,B',\ldots\}$ if for every block $B \in \pi$ , there is a block $C \in \sigma$ such that $B \subseteq C$ . The partitions on U are partially ordered by refinement with the minimum partition or bottom being the indiscrete partition $0_{U}=\{U\}$ , nicknamed the “blob,” consisting of U as a single block, and the maximum partition or top being the discrete partition $1_{U}=\{\{u\}\{u'\},\ldots\}$ where each block is a singleton.

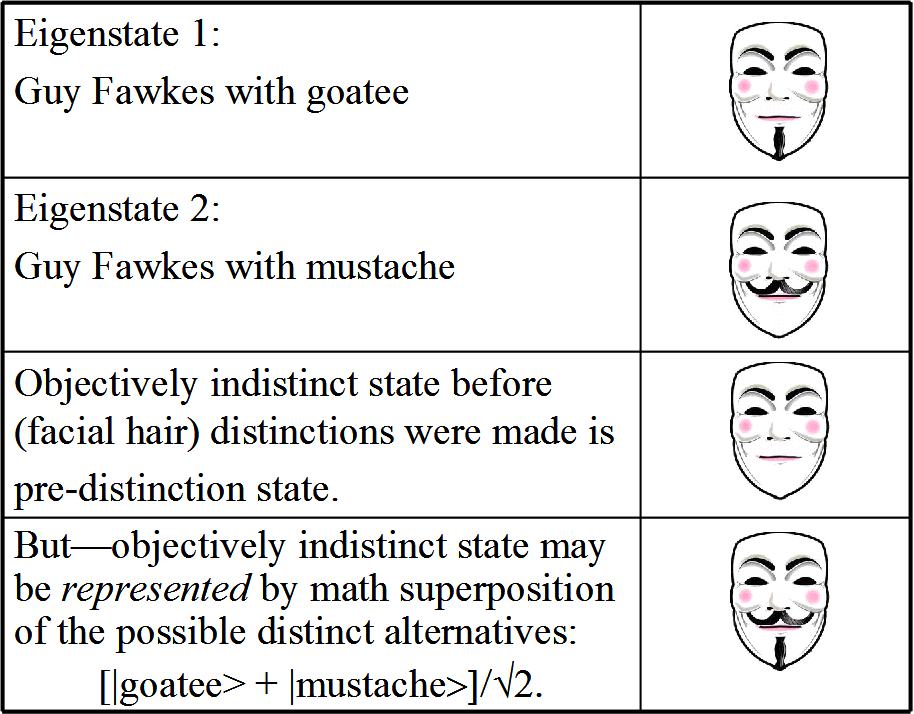
The elements of U are to be thought of as fully distinct elements. But the key idea of the objective indefiniteness idea is to interpret each nonsingleton subset $S \subseteq U$ , e.g., a block in a partition, not as a set of definite elements, but as a single objectively indefinite element. The single indefinite element will become more definite as more distinctions are made until it finally reaches one of the fully definite elements $\{u\}$ where $u\in U$ . The singleton $\{u\}$ should be thought as just designating the element u.

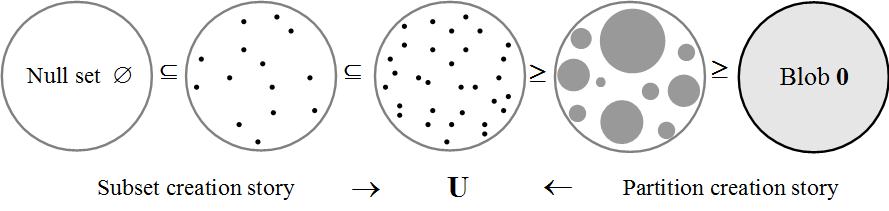
There are two abstract “creation stories” obtained by starting at the bottom of each lattice and moving to the top. The two tops are essentially the same universe U.

Subset creation story: “In the Beginning was the Void”, and then elements are created, fully propertied and distinguished from one another, until finally reaching all the elements of the universe set U.
Partition creation story: “In the Beginning was the Blob”, which is an undifferentiated “substance,” and then there is a “Big Bang” where elements (“its”) are created by being objectively in-formed (objective “dits”) by the making of distinctions (e.g., breaking symmetries) until the result is finally the singletons that designate the elements of the universe U.

The two creation stories could be illustrated as follows:

One might think of the universe U (in the middle of the above picture) as the macroscopic world of fully definite entities that we ordinarily experience. Common sense and classical physics assumes, as it were, the subset creation story on the left. But a priori, it could just as well have been the dual story, the partition creation story pictured on the right, that leads to the same macro-picture U. And, as we show in the paper, that is indeed the message of quantum mechanics.

The conceptual duality between the subset and partition lattices can also be expressed using the metaphysical notions of “substance” and “form.”

At the bottom of the Boolean lattice is the empty set $\emptyset$ which represents no substance. As one moves up the lattice, new fully propertied elements of substance appear until finally one reaches the top, the universe U. Thus new substance is created but each element is fully formed and distinguished in terms of its properties.

At the bottom of the partition lattice is the blob 0 which represents all the substance but with no distinctions to in-form the substance. As one moves up the lattice, no new substance appears but distinctions objectively in-form the indistinct elements as they become more and more distinct, until one finally reaches the top, the discrete partition 1, where all the elements of U have been fully distinguished from each other. Thus one ends up at the same place either way, but by two totally different but dual ways.

Heisenberg identifies the “substance” with energy.

Energy is in fact the substance from which all elementary particles, all atoms and therefore all things are made, and energy is that which moves. Energy is a substance, since its total amount does not change, and the elementary particles can actually be made from this substance as is seen in many experiments on the creation of elementary particles.[Heisenberg 1958, p. 63]

In his sympathetic interpretation of Aristotle’s treatment of substance and form, Heisenberg refers to the substance as: “a kind of indefinite corporeal substratum, embodying the possibility of passing over into actuality by means of the form.” [Ibid., p. 148] Heisenberg’s “possibility … passing over into actuality by means of the form” should be seen as the actual indefinite “passing over into” the actual definite by being objectively in-formed through the making of distinctions.

A few more images might help to develop the mental imagery to make the notion of objective indefiniteness more intuitive. Even though a superposition, as an objectively indefinite element, should be thought of as a pre-distinction state, one still needs to specify which fully definite elements it might become when distinctions are made. Perhaps the following graphs will be helpful.

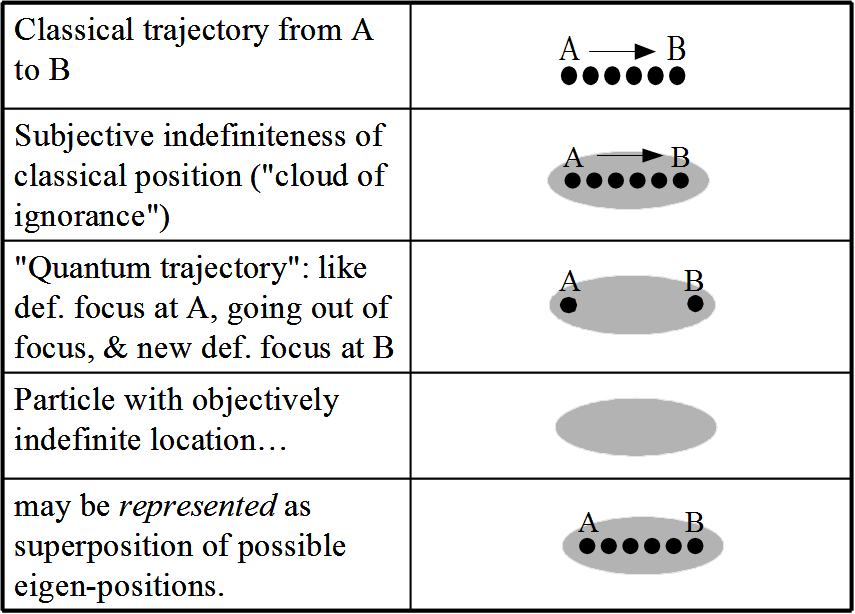
The following table gives yet another attempt at visualization by contrasting a classical picture and an objectively indefinite (or “quantum”) picture of a “particle” getting from A to B.

The classical trajectory is a sequence of definite positions. A state of subjective indefiniteness is compatible with a classical trajectory when we have a “cloud of ignorance” about the actual definite location of the particle. The “quantum trajectory” might be envisaged as starting with a definite focus or location at A, then evolving to an objectively indefinite state (with the various positions as possible definite foci), and then finally another “look” or measurement that achieves a definite focus at location B. The particle in its objectively indefinite position state is represented as the superposition of the possible definite position states.

The lifting program

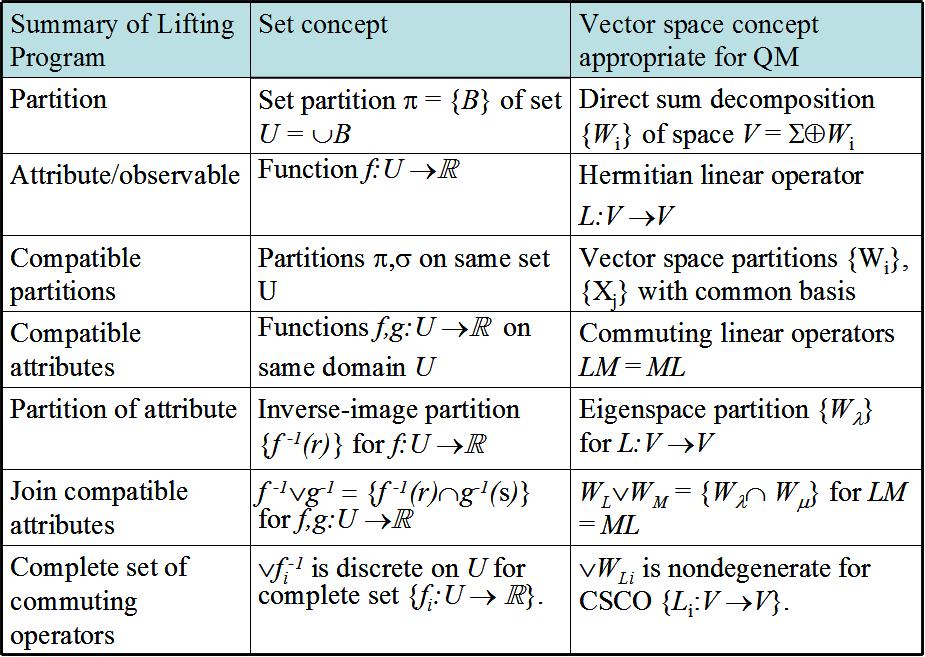
The concepts from partition logic and logical information theory are all formulated in the rather simple and austere environment of sets. They need to be “lifted” to the mathematically rich environment of vector spaces where quantum mechanics lives. This relationship between sets and vector spaces is part of the mathematical folklore, although it is not a algorithm nor a one-to-one mapping between concepts.

The guiding principle is the basis principle: apply a set concept to the basis set of a vector space and then “generate” the corresponding vector space concept. For instance, apply the set notion of cardinality to a basis set, and we obtain not the cardinality of the vector space but its dimension. Thus the vector space concept of dimension is the lift of the set concept of cardinality.

In view of the central role of partitions, a key question is the lift of the notion of a partition on a set. Taking a set partition of a basis set for a vector space, the blocks in the partition generate subspaces that together form a direct sum decomposition of the vector space (which is very different from a set partition of a vector space).

In Boolean logic, we have the notion of a property which is something that an element definitely has or does not have. In partition logic, the corresponding notion is an attribute which is something that all elements have but with various values (e.g., the height or weight of a person). Technically, an attribute is give by a function $f:U\rightarrow R$ for some value set R (in our context it would be the real numbers). Since we are lifting the notions of partition logic to vector spaces, what is the lift of an attribute? A real-valued attribute f assigns a constant real number to each block $f^{-1}(r)$ of a set partition. Hence the lifted concept would have to assign a real number to each block (subspace) in a vector space partition (direct sum decomposition). The vector space concept that does that is a Hermitian linear operator on the space where the real values are the eigenvalues and the subspaces are the eigenspaces of the operator.

The paper can be consulted for the other lifts which are summarized in the following table.

The important thing is that when the set concepts from partition logic are lifted to vector spaces, then one immediately gets part of the mathematical machinery of quantum mechanics (e.g., Hermitian operators and complete sets of commuting operators determining eigenstates). But what about the Schrödinger wave equation and all that?

Waving good-by to waves

The objective indefiniteness interpretation incorporates and explains the recognition that there are no actual physical waves in QM (e.g., the amplitudes are complex numbers). Hence the interpretation needs to offer reformulations of such ideas as “wave-particle duality.”

The indistinctness-represented-as-superpositions is usually interpreted as “wave-like aspects” of the particles in the indefinite state. Hence the distinction-making measurements take away the indistinctness–which is usually interpreted as taking away the “wave-like aspects,” i.e., “collapse of the wave packet.” There are no actual physical waves in quantum mechanics, only particles with indistinct attributes for certain observables. Thus the “collapse of the wave packet” is better described as the “collapse of indefiniteness” to achieve definiteness. And the “wave-particle duality” is actually the indistinct-distinct particle duality or complementarity.

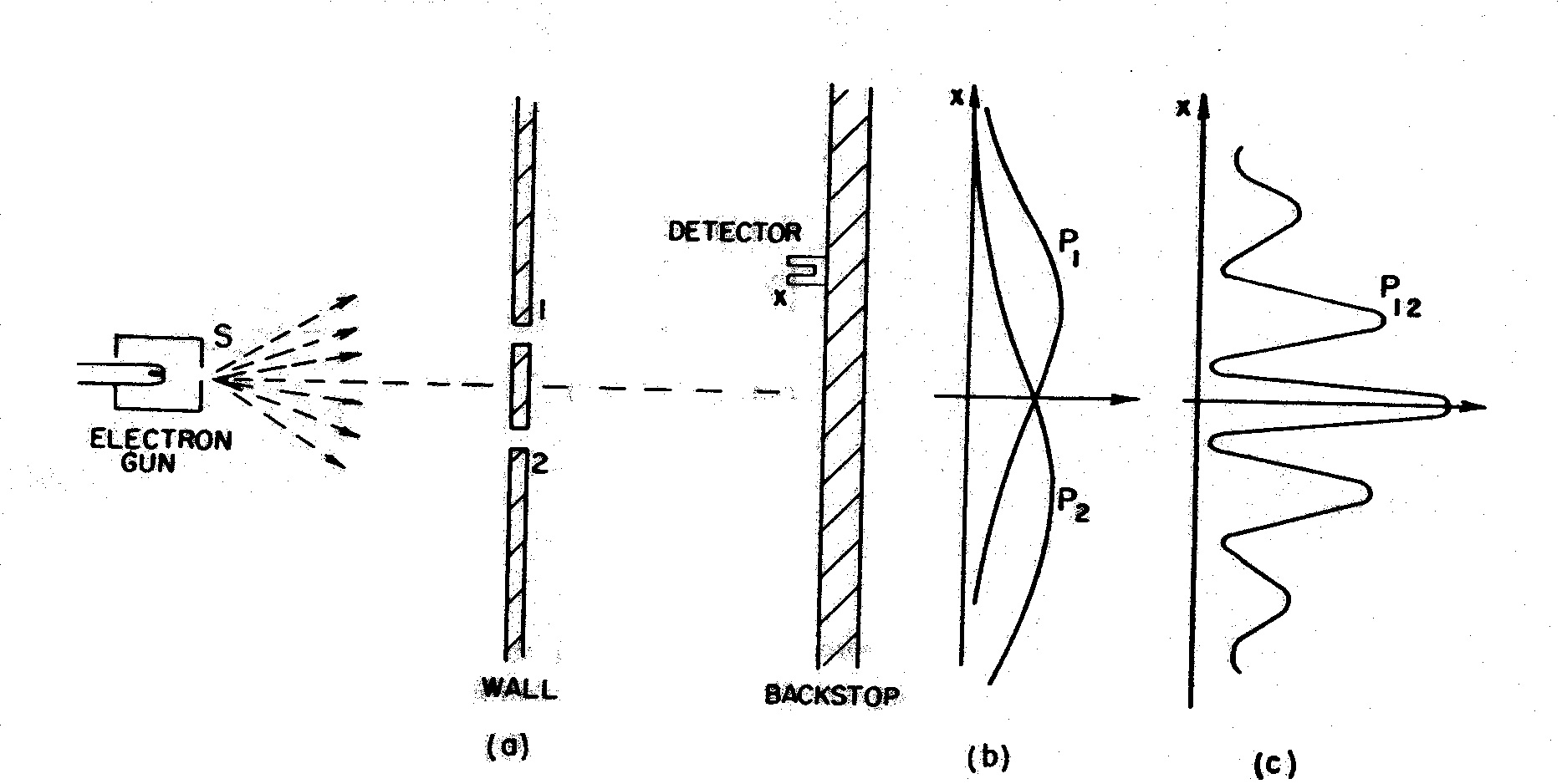
Consider the standard double-slit experiment. When there is no distinction between the two slits, then the position attribute of the traversing particle is indefinite, neither top slit nor bottom slit (not “going through both slits”), which is usually interpreted as the “wave-like aspects” that show interference. But when a distinction is made between the slits, e.g., inserting a detector in one slit or closing one slit, then the distinction reduces the indefiniteness to definiteness so the indefiniteness disappears, i.e., the “wave-like aspects” disappear. For instance, Feynman makes this point about distinctions in terms of distinguishing the alternatives or “final states” (such as “traversing top slit” or “traversing bottom slit”).

If you could, in principle, distinguish the alternative final states (even though you do not bother to do so), the total, final probability is obtained by calculating the probability for each state (not the amplitude) and then adding them together. If you cannot distinguish the final states even in principle, then the probability amplitudes must be summed before taking the absolute square to find the actual probability.[Feynman 1965, p. 3.9]

What about the Schrödinger wave equation? Since measurements, or, more generally, interactions between a quantum system and the environment, may make distinctions (measurement and decoherence), we might ask the following question. What is the evolution of a quantum system that is isolated so that not only are no distinctions made, but even the degree of indistinctness between state vectors is not changed? Two states $\psi$ and $\phi$ in a Hilbert space are fully distinct if they are orthogonal, i.e., $\langle \psi|\phi\rangle = 0$ . Two states are fully indistinct if $\langle \psi|\phi\rangle = 1$ . In between, the degree of indistinctness can be measured by $\langle \psi|\phi\rangle$ , the inner product of the state vectors. Hence the evolution of as isolated quantum system where the degree of indistinctness does not change is described by a linear transformation that preserves inner products, i.e., a unitary transformation.

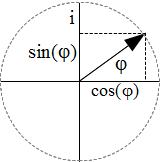
In simplest terms, a unitary transformation describes a rotation such as the rotation of the unit vector in the complex plane.

The rotating unit vector traces out the cosine and sine functions on the two axes, and the position of the arrow can be compactly described as a function of $\phi$ using Euler’s formula:

$e^{i\phi} = cos(\phi) + i sin(\phi)$ .

But this is the formula describing a complex “wave” in a one-dimensional Hilbert space. In general, the mathematics describing the degree-of-indistinctness-preserving evolution of an isolated system (i.e., the context where Schrödinger’s equation holds) is the mathematics of complex “waves.” The “wave” solutions to Schrodinger’s equation describe the evolution of particles in indefinite states when there are no interactions to change the degree of indistinctness between states. Thus the objective indefiniteness approach to interpreting QM provides an explanation for the appearance of the “wave mathematics” (which implies interference as well as the quantized solutions to the “wave” equation that gave the theory its name) when, in fact, there are no actual physical waves involved.

Measurement and composite systems

The next step is to lift the partition mathematics to describe measurement. That is where the new logical information theory comes into play. Logical entropy generalizes easily to the quantum logical entropy of a density matrix $\rho$ . A measurement is a distinction-making procedure that in the “nondegenerate” case refines an indefinite state into one of the possible fully definite eigenstates (of the observable being measured). In a degenerate measurement, distinctions are also made so the indefinite state becomes more definite but not a fully definite eigenstate. In each case, the distinctions being made are registered in the off-diagonal “coherence” terms in the density matrix being zeroed or “decohered” to obtain the post-measurement density matrix. The quantum logic entropy turns out to be precisely the sum of the absolute squares of those decohered terms, so the lifted notion of the logical entropy precisely fits the quantum case by “measuring” the measurement.

When we have two sets U and U’ and want to form the composite set, we form the direct or Cartesian product $U\times U'$ . In the lifted case, we have two vector spaces representing two quantum systems, and we want to form the composite space to represent the composite system. By the basis principle, we take the Cartesian product of the two basis sets for the two spaces and generate the composite vector space from the elements in that Cartesian product. The result is the tensor product (not the direct product) of the spaces, and that is indeed the space used in QM to represent composite systems.

In this manner, we derive the mathematical framework and the relationships of the axioms of quantum mechanics (see paper for details).

Conclusion

The objective indefiniteness interpretation of quantum mechanics is based on using partition logic, logical information theory, and the lifting program to fill out the back story to the old notion of “objective indefiniteness” [Shimony 1988, 1989].

At the level of sets, if we start with a universe set U as representing our common-sense macroscopic world, then there are only two logics, the logics of subsets and quotient sets (i.e., partitions), to envisage the “creation story” for U. Increase the size of subsets or increase the refinement of quotient sets until reaching the universe U. That is, starting with the empty subset of U, take larger and larger subsets of well-defined fully definite elements until finally reaching all the fully definite elements of U. Or starting with the indiscrete partition on U, take more and more refined partitions, each block interpreted as an indefinite element, until finally reaching all the fully definite elements of U.

Classical mechanics was fully compatible with the subset creation story, where elements were always fully propertied (“properties all the way down”). But almost from the beginning, quantum mechanics was seen not to be compatible with that world view of always fully definite entities; QM seems to envisage entities at the micro-level that are objectively indefinite. Within the framework of the two logics given by subset-partition duality, the “obvious” thing to do is to elaborate on the other creation story to try to build the other interpretation of QM.

With the development of the logic of partitions (dual to the logic of subsets) and logical information theory built on top of it, the foundation was in place to lift those set concepts to the richer mathematical environment of vector spaces (Hilbert spaces in particular). In that manner, the other interpretation of QM was constructed. Unlike the interpretation based on entities with fully definite properties expressed by Boolean subset logic, the other interpretation works. That is, the result reproduces the basic ideas and mathematical machinery of quantum mechanics. Thus there is no need for desperate flights of fancy to try to interpret quantum mechanics. Just use the other logic that is dual to Boolean subset logic, and it works. Period.

References

Britz, Thomas, Matteo Mainetti and Luigi Pezzoli 2001. Some operations on the family of equivalence relations. In Algebraic Combinatorics and Computer Science: A Tribute to Gian-Carlo Rota. Henry Crapo and Domenico Senato eds., Milano: Springer: 445-59.

Church, Alonzo 1956. Introduction to Mathematical Logic. Princeton: Princeton University Press.

Feynman, Richard P., Robert B. Leighton and Matthew Sands 1965. The Feynman Lectures on Physics: Quantum Mechanics (Vol. III). Reading MA: Addison-Wesley.

Finberg, David, Matteo Mainetti and Gian-Carlo Rota 1996. The Logic of Commuting Equivalence Relations. In Logic and Algebra. Aldo Ursini and Paolo Agliano eds., New York: Marcel Dekker: 69-96.

Heisenberg, Werner 1958. Physics & Philosophy: The Revolution in Modern Science. New York: Harper Torchbooks.

Lawvere, F. William and Robert Rosebrugh 2003. Sets for Mathematics. Cambridge: Cambridge University Press.

Shimony, Abner 1988. The reality of the quantum world. Scientific American. 258 (1): 46-53.

Shimony, Abner 1989. Conceptual foundations of quantum mechanics. In The New Physics. Paul Davies ed., Cambridge: Cambridge University Press: 373-395.