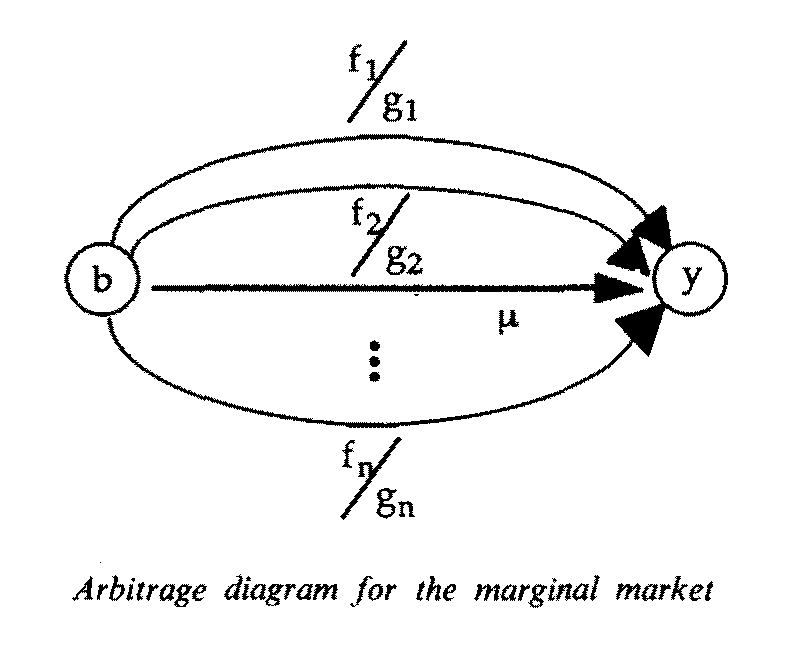
The paper mathematically develops the heuristic idea that the first-order necessary conditions for a classical constrained optimization problem are equivalent to a market being arbitrage-free – with the Lagrange multipliers being the arbitrage-free market prices. The arbitrage notions start with the multiplicative Kirchhoff’s Voltage Law and then generalize to matrix algebra. The basic result shows the normalized arbitrage-free «market prices» (the Lagrange multipliers) resulting from a classical constrained optimization problem can always be obtained as a ratio of cofactors. The machinery also gives an economic interpretation of Cramer’s Rule as a competitive equilibrium condition. Thus one can “find the markets in the math” of a classical constrained optimization problem.
Click here to download the paper.