In this paper, I am publishing for the first time the author’s devil’s advocacy document when I was Senior Advisor to the Chief Economist of the World Bank, Joseph Stiglitz.
The Basic Ideas of Quantum Mechanics
September 19, 2025 by
For a century, quantum theorists have been reading the mathematical entrails of quantum mechanics (QM) to divine the nature of quantum reality. But to little avail. Let’s try a new approach.
The Mean and Variance as Dual Concepts
June 16, 2025 by
This paper gives a new derivation of the variance (and covariance) based on the two-sample approach, which positions the variance on the partition and information theory side of the duality and thus dual to the mean.
Generative Mechanisms
June 10, 2025 by
The purpose of this paper is to abstractly describe the notion of a generative mechanism
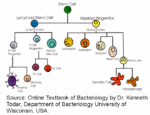
that implements a code and to provide a number of examples including the DNA-RNA machinery that
implements the genetic code, Chomsky’s Principles & Parameters model of a child acquiring a specific
grammar given ‘chunks’ of linguistic experience (which play the role of the received code), and embryonic
development where positional information in the developing embryo plays the role of the received code.
Are Corporations the Problem?
May 26, 2025 by
Are corporations the problem? Can reforms in the area of corporate responsibility (e.g., more stakeholder governance) lead to any real changes? The goal of the paper is to analyse debates concerning the Citizens United case, corporate personhood, the stakeholder theory, the affected interests principle and, finally, deeper fallacies with respect to the rights of capital embedded in Marxism and conventional economic theories of capital and corporate finance.
Classical Liberalism and the Abolition of Certain Voluntary Contracts
May 19, 2025 by
This paper analyzes three contracts and shows that there is indeed a deeper democratic or Enlightenment classical liberal tradition of jurisprudence that rules out those contracts. The ‘problem’ is that the same principles imply the abolition of the employment contract, the contract for renting human beings, which is the foundation for the economic system that is often (but superficially) identified with classical liberalism itself. Frank Knight is taken throughout as the exemplary advocate of the economics of conventional classical liberalism.
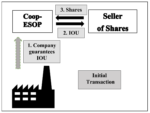
Worker Cooperatives and Other “Cooperatives”
March 24, 2025 by
When is a “Coop” not really a cooperative? The short answer is whenever the actual activity of the “cooperative” is not carried out by the members but by employees. The problem is, of course, not in cooperation per se but in the hiring, employing, renting, or leasing of people to carry out the supposedly “cooperative” activities of the “cooperative.”
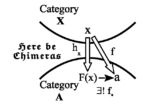
Where do Adjunctions come from?
March 19, 2025 by
Category theory has foundational importance because it provides conceptual lenses to characterize what is important and universal in mathematics—with adjunction seeming to be the primary lens. Our topic is a theory showing “where adjoints come from”.
Born Again! The Born Rule as a Feature of Superposition
March 18, 2025 by
Where does the Born Rule come from? We ask: “What is the simplest extension of probability theory where the Born rule appears”? This is answered by introducing “superposition events” in addition to the usual discrete events.
Fallacies about corporations
March 15, 2025 by
This article comments on Isabelle Ferreras’s “Democratizing the Corporation.” The focus is on the conceptual framing, which arguably contains a number of problems that are quite common on the left and are thus doubly deserving of commentary and explanation.