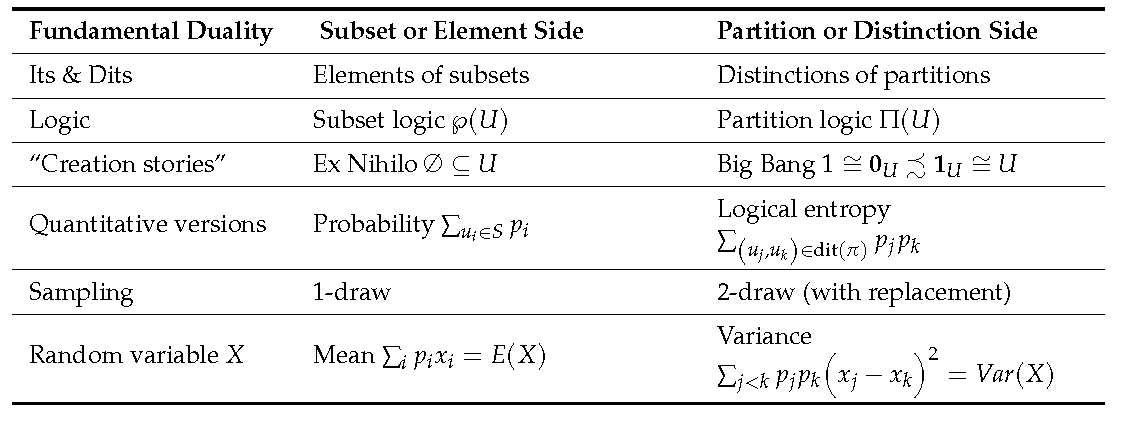
A basic duality arises throughout the mathematical and natural sciences. Traditionally, logic is thought to be based on the Boolean logic of subsets, but the development of category theory in the mid-twentieth century shows the duality between subsets and partitions (or equivalence relations). Hence, there is an equally fundamental dual logic of partitions. At a more basic or granular level, the elements of a subset are dual to the distinctions (pairs of elements in different blocks) of a partition. The quantitative version of subset logic is probability theory (as developed by Boole), and the quantitative version of the logic of partitions is information theory re-founded on the notion of logical entropy. The subset side of the duality uses a one-sample (or one-element) approach, e.g., the mean of a random variable; the partition side uses a two-sample (or pair-of-elements) approach. This paper gives a new derivation of the variance (and covariance) based on the two-sample approach, which positions the variance on the partition and information theory side of the duality and thus dual to the mean.