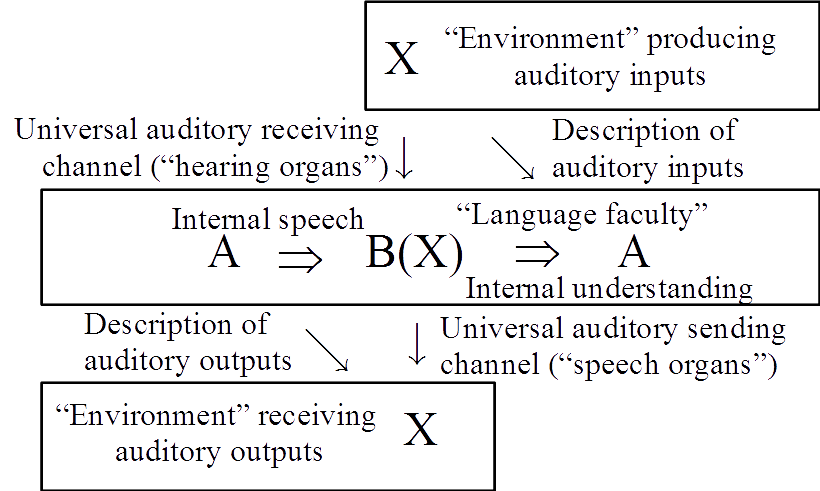This is a preprint of a paper forthcoming in Axiomathes and already in Online First for that journal.
There is some consensus among orthodox category theorists that the concept of adjoint functors is the most important concept contributed to mathematics by category theory. We give a heterodox treatment of adjoints using heteromorphisms (object-to-object morphisms between objects of different categories) that parses an adjunction into two separate parts (left and right representations of heteromorphisms). Then these separate parts can be recombined in a new way to define a cognate concept, the brain functor, to abstractly model the functions of perception and action of a brain. The treatment uses relatively simple category theory and is focused on the interpretation and application of the mathematical concepts.
The Mathematical Appendix is of more general interest to category theorists since it is a defense of the use of heteromorphisms in general in category theory.