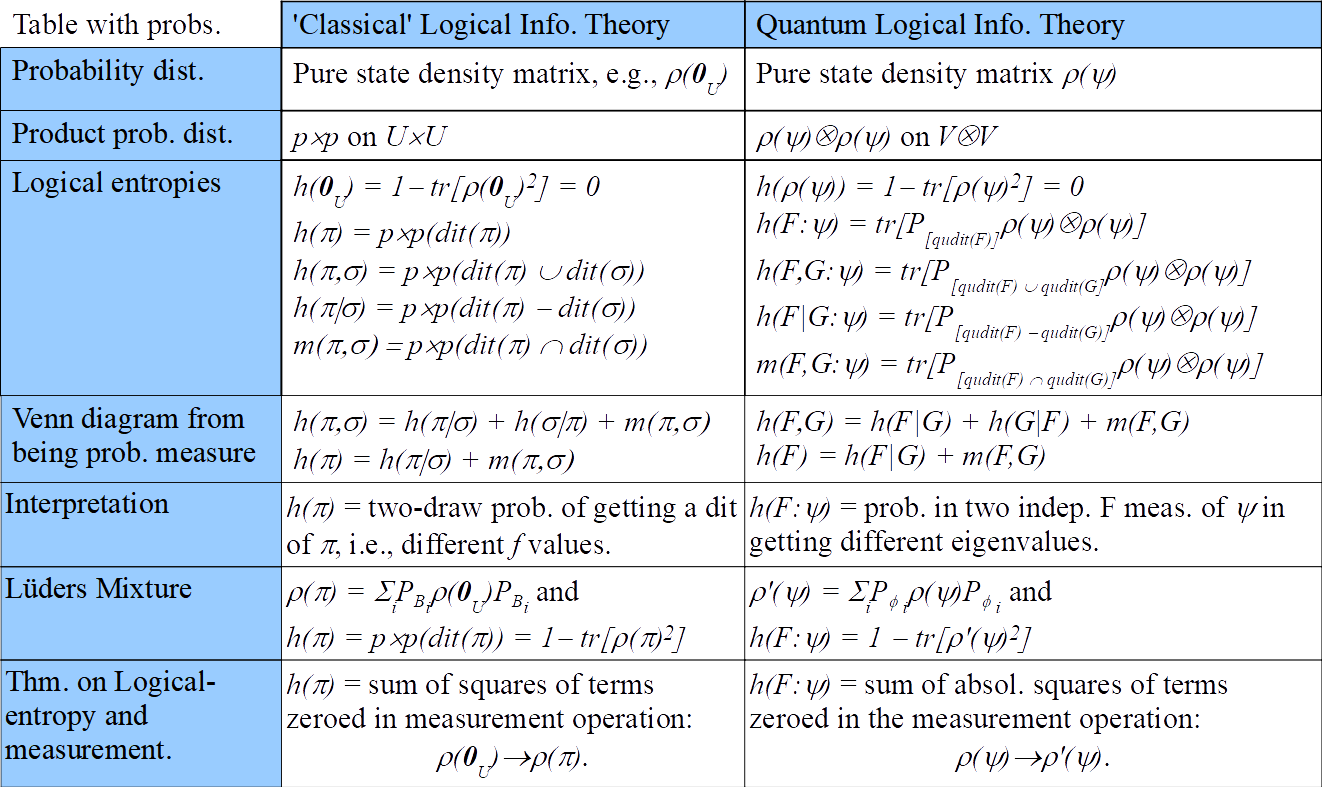
Logical information theory is the quantitative version of the logic of partitions just as logical probability theory is the quantitative version of the dual Boolean logic of subsets. The resulting notion of information is about distinctions, differences, and distinguishability, and is formalized using the distinctions (`dits’) of a partition (a pair of points distinguished by the partition). All the definitions of simple, joint, conditional, and mutual entropy of Shannon information theory are derived by a uniform transformation from the corresponding definitions at the logical level.
The purpose of this paper is to give the direct generalization to quantum logical information theory that similarly focuses on the pairs of eigenstates distinguished by an observable, i.e., qudits of an observable. The fundamental theorem for quantum logical entropy and measurement establishes a direct quantitative connection between the increase in quantum logical entropy due to a projective measurement and the eigenstates (cohered together in the pure superposition state being measured) that are distinguished by the measurement (decohered in the post-measurement mixed state). Both the classical and quantum versions of logical entropy have simple interpretations as “two-draw” probabilities for distinctions. The conclusion is that quantum logical entropy is the simple and natural notion of information for quantum information theory focusing on the distinguishing of quantum states.
Click here to download the reprint from the Entropy journal.